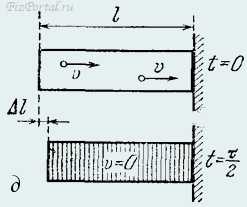
Оценить время упругого удара твердых тел, рассматривая столкновение стержня, налетающего торцом на неподвижную недеформируемую стенку (рис.).
Чаще всего в задачах считают, что упругий удар твердых тел происходит мгновенно, но совершенно очевидно, что это предположение является идеализацией. Столкновение реальных тел всегда занимает конечный промежуток времени τ. В самом деле, если бы изменение импульса тела при столкновении происходило мгновенно,F = mΔv/t→0 → ∞ то сила взаимодействия тел при ударе была бы бесконечно большой, чего, естественно, не бывает. От чего же может зависеть длительность столкновения? Допустим, что мы рассматриваем отражение упругого тела от недеформируемой стенки. При столкновении кинетическая энергия тела в течение первой половины столкновения превращается в потенциальную энергию упругой деформации тела. В течение второй половины происходит обратное превращение энергии деформации в кинетическую энергию отскакивающего тела.Поэтому очевидно, что упругие свойства тела играют определенную роль при столкновении. Итак, можно ожидать, что длительность удара зависит от модуля Юнга материала тела Е, его плотности ρ и его геометрических размеров. Возможно, что длительность удара τ зависит и от скорости v, с которой тело налетает на преграду. Нетрудно убедиться, что оценить время столкновения с помощью одних только соображений размерности не удастся. Действительно, если даже взять в качестве налетающего тела шар, размеры которого характеризуются только одним параметром − радиусом R, то из величин Е, ρ, R и v можно составить бесчисленное множество выражений, имеющих размерность времени:
| Обратная связь | МЕХАНИЧЕСКИЙ УДАР
Нижний Новгород2013 год
Лабораторная работа № 1-21 Механический удар Цель работы: Ознакомиться с элементами теории механического удара и экспериментально определить время удара , среднюю силу удара F, коэффициент восстановления Е, а также изучить основные характеристики удара и ознакомиться с цифровыми приборами для измерения временного интервалов.
Теоретическая часть
рис.1 Пусть на плоскую поверхность массивной пластины падает шар с некоторой скоростью V1 и отскакивает от нее со скоростью V2. Обозначим – нормальные и тангенциальные составляющие скоростей и , а и – соответственно углы падения и отражения. В идеальном случае при абсолютно упругом ударе, нормальные составляющие скоростей падения и отражения и их касательные составляющие были бы равны ; . При ударе всегда происходит частичная потеря механической энергии. Отношение как нормальных, так и тангенциальных составляющих скорости после удара к составляющим скорости до удара есть физическая характеристика, зависящая от природы сталкивающихся тел. (1) Эту характеристику Е называют коэффициентом восстановления. Числовое значение его лежит между 0 и 1. Определение средней силы удара, Начальной и конечной скоростей шарика при ударе
На основании теоремы об изменении импульса материальной точки: (2) где и – векторы скоростей шара до и после удара; τ – длительность удара. После проектирования уравнения (2) на горизонтальную ось определим среднюю силу удара: (3) Скорости шарика V1 и V2 определяются на основании закона сохранения и превращения энергии. Изменение механической энергии системы, образованной шариком и неподвижным телом В, в поле тяготения Земли определятся суммарной работой всех внешних и внутренних не потенциальных сил. Поскольку внешняя сила перпендикулярна перемещению и нить нерастяжима, то эта сила работы не совершает, внешняя сила и внутренняя сила упругого взаимодействия – потенциальны. Если эти силы много больше других не потенциальных сил, то полная механическая энергия выбранной системы не меняется. Поэтому, уравнение баланса энергии можно записать в виде: (4) Из чертежа (рис. 2) следует, что , тогда из уравнения (4) получим значения начальной V1 и конечной V2 скоростей шарика: (5) где и - углы отклонения шара до и после соударения.
Метод определения длительности удара
В данной работе длительность удара шарика о плиту определяется частотомером Ч3-54, функциональная схема которого представлена на рис.3. С генератора подается на вход системы управления СУ импульсы с периодом Т. Когда в процессе соударения металлической плиты В, электрическая цепь, образованная СУ, проводящими нитями подвеса шара, шаром, плитой В и счетчиком импульсов Сч, оказывается замкнутой, и система управления СУ пропускает на вход счетчика Сч импульсы электрического тока только в интервале времени , равном времени длительности удара. Число импульсов, зарегистрированных за время , равно , откуда . Чтобы определить длительность удара , необходимо число импульсов, зарегистрированных счетчиком, умножить на период импульсов, снимаемых с генератора Г.
Экспериментальная часть Исходные данные: 1. Масса шарика m = (16,7 ± 0,1)*10-3 кг. 2. Длина нити l = 0,31 ± 0,01 м. 3. Ускорение свободного падения g = (9,81 ± 0,005) м/с2. 4. Опыт для каждого угла выполняем 5 раз.
Результаты опыта занесем в таблицу:
Расчёты =200 мкс 0,6054 м/с 0,5148 м/с =300 мкс 0,9026 м/с 0,8064 м/с =400 мкс 1,1928 м/с 1,0927 м/с =500 мкс 1,4739 м/с 1,3357 м/с =600 мкс 1,7438 м/с 1,6839 м/с и –скорости шарика до и после удара. < > – среднее значение силы удара. <> – средняя длительность удара. Е – коэффициент восстановления. Результаты расчетов
| |
pdnr.ru
Cтраница 1
Время удара т делится на два периода ( т т: тз): первый период - от момента соприкасания до момента наибольшего сближения; второй период - от момента наибольшего сближения до момента разъединения. [1]
Время удара тесно связано с продолжительностью деформации грунта и потому зависит от тех же факторов, которые влияют на эту продолжительность. Сюда нужно отнести величину самой деформации и скорость ее течения. Та деформация, которая успевает развиться за время удара, определяется степенью податливости грунта внешним нагрузкам и потому зависит от вида и состояния грунта и в первую очередь от его плотности и влажности. Величина деформации зависит также от интенсивности воздействия на грунт внешней нагрузки, поэтому деформация и время удара растут по мере увеличения массы штампа, высоты его падения и удельного импульса. [2]
Время удара т делится на два периода ( т T. [3]
Время удара т делится на два периода ( т TI 2) - 1 - й период - от момента соприкасания до момента наибольшего сближения; 2 - й период - от момента наибольшего сближения до момента разъединения. [4]
Время удара при исследовании было менее 0 1 с, что по существу исключает нормальную реакцию оператора на аварийный останов. Необходимость такого останова нуждается в специальном исследовании при конкретных параметрах машины. [6]
Время удара капли воды диаметром 3 6 мм составляет 0 024 о. [7]
Время удара буквенного рычага о фетровую подушку не учитывается, так как очередной удар по клавише происходит в момент соприкосновения рычага с подушкой. [8]
Если время удара значительно меньше периода движения, то достаточную точность обычно обеспечивает модель абсолютно твердого тела. Но даже в этой упрощенной постановке исследование возможных режимов движения в зависимости ог значений параметров процесс весьма трудоемкий, и поэтому можно рекомендовать инженеру, проектирующему ударно-вибрационные машины, самому этими расчетами не заниматься. [9]
Во время удара равновесие этих сил нарушается, и появляются новые силы, например силы трения. Однако во время самого удара все эти силы можно не принимать во внимание, так как они пренебрежимо малы по сравнению с силой, которая действует на маятник со стороны налетающих на него пули и снаряда. [10]
Во время удара шаблон легко может переместиться и точность разметки нарушится. Поэтому при этом способе разметки отверстий рекомендуется прикреплять шаблон к изделию небольшими струбцинами, как это показано на фиг. При наличии автоматического кернера необходимость в прикреплении шаблонов отпадает, так как накернивать центры отверстий можно одной рукой, а другой в это время придерживать шаблон. [11]
Во время удара производная - jr, изменяясь непрерывно, меняет свой знак при переходе через нуль. [12]
Во время удара оба тела претерпевают изменение формы ( деформацию), процесс удара можно разделить на две фазы. В течение первой фазы происходит сближение тел; оба тела производят работу против сил реакции; их кинетическая энергия уменьшается; относительная скорость ( в момент встречи она не равна нулю, иначе не было бы удара) уменьшается до нуля, чем первая фаза и заканчивается. Вслед за этим наступает вторая фаза: тела начинают удаляться друг от друга, восстанавливая свою форму, при этом реакции совершают положительную работу, живая сила системы растет, относительная скорость, переменив знак, возрастает по абсолютной величине, наконец, тела отделяются, этим и заканчивается процесс удара. [13]
Поскольку время удара пренебрежимо мало, то перемещения точек тела за время удара также пренебрежимо малы, поэтому принято считать, что координаты точек тела во время удара остаются постоянными. [14]
Во время удара клапан опирается на резиновое кольцо 2, которое смягчает механический удар и улучшает закрытие отверстия истечения. [15]
Страницы: 1 2 3 4
www.ngpedia.ru
Явление, при котором за очень малый промежуток времени скорости точек тела изменяются на конечную величину, называется ударом. Силы, возникающие при таком взаимодействии, называются ударными.
Ударная сила F достигает значительной величины. Импульс ударной силы называется ударным импульсом и является конечной величиной:
где τ – продолжительность удара (очень малый промежуток времени, в течение которого происходит удар).
В теории удара принимаются следующие основные допущения:
В теории удара применяют теорему об изменении количества движения материальной точки: изменение количества движения материальной точки за время удара равно действующему на эту точку ударному импульсу
где m – масса точки, ν – скорость точки до удара, u – скорость точки после удара.
При проекции на координатные оси можно получить три скалярных уравнения:
Для механической системы, состоящей из n точек, уравнение (2) можно представить в виде
где m – масса k-той точки, νk и uk – скорости k-той точки соответственно до и после удара, Sk(e) – равнодействующая всех внешних ударных импульсов, приложенных к k-той точке.
Теорема об изменении количества движения механической системы при ударе звучит так: изменение количества движения механической системы за время удара равно геометрической сумме всех внешних ударных импульсов, действующих на эту систему.
Уравнение (4) можно записать в виде
где m – масса всей системы, νc и uc – скорости центров масс системы соответственно в начале и в конце удара.
В проекциях на координатные оси получаем:
mucx — mνcx = ∑Skx(e),mucy — mνcy = ∑Sky(e), (6)mucz — mνcz = ∑Skz(e).
Теорема об изменении кинетического момента при ударе формулируется следующим образом: изменение кинетического момента механической системы за время удара относительно какого-либо центра равно геометрической сумме моментов всех внешних ударных импульсов, действующих на эту систему относительно того же центра
где L0(1) и L0(2) – кинетические моменты системы относительно центра соответственно до и после удара:
∑M0Sk(e) – сумма моментов внешних ударных импульсов относительно точки O:
В проекциях на координатные оси уравнение (7) принимает вид:
Кинетическая энергия до удара для двух соударяющихся точек или тел, движущихся поступательно, записывается в виде
T0 = ½m1v12 + ½m2v22, (9)
где v1 и v2 – скорости соударяющихся точек или тел до удара.
Кинетическая энергия точек или тел, движущихся поступательно, после удара равна
T = ½m1u12 + ½m2u22, (10)
где u1 и u2 – скорости точек или тел после удара.
При ударе двух тел различают две стадии удара. Первая стадия: тела входят в контакт друг с другом и после этого центры масс их продолжают сближаться за счет деформации тел (упругих и пластических). Первая стадия – стадия деформации – заканчивается тогда, когда деформации обоих тел достигают максимального значения.
Вторая стадия – стадия восстановления: упругие свойства тел, если они имели место, заставляют центры масс удаляться друг от друга. В то время как пластические деформации (если они имели место) остаются. Упругие деформации полностью исчезают и тела начинают двигаться порознь.
Степень восстановления формы тел зависит от упругих свойств материалов этих тел и характеризуется соотношением скоростей тел до и после удара.
Ньютоном введен коэффициент восстановления при ударе, величина которого определяется по формуле
k = u/v, 0<k<1, (11)
где v и u – относительные скорости соударяющихся тел соответственно до и после удара.
Если тело падает с высоты H и после удара о неподвижную поверхность поднимается на высоту h, то коэффициент восстановления равен
Если удар абсолютно упругий, то соударяющиеся тела полностью восстанавливают свою форму, при этом k = 1. Если удар абсолютно неупругий, то тела на второй стадии не восстанавливают свою форму, при этом k = 0.
Промежуточные значения соответствуют случаям не вполне упругого удара. Случай абсолютно упругого удара (k = 1) имеет лишь теоретическое значение. В зависимости от материала соударяющихся тел коэффициент восстановления имеет различные значения.
Примеры решения задач по динамике >>
isopromat.ru
Cтраница 2
Если время удара значительно меньше периода движения, то достаточную точность обычно обеспечивает модель абсолютно твердого тела. Но даже в этой упрощенной постановке исследование возможных режимов движения в зависимости ог значений параметров процесс весьма трудоемкий, и поэтому можно рекомендовать инженеру, проектирующему ударно-вибрационные машины, самому этими расчетами не заниматься. [16]
За время удара связи могут сохраняться, но могут и не сохраняться. Будем называть связь сохраняющейся, если она существует во время удара и сохраняется после удара. [17]
Во время удара ресничек действие его подобно вращению колеса. Тело коловраток делится на три отдела: головку, увенчанную вращательным аппаратом; туловище, часто покрытое достаточно толстой, но прозрачной кожицей и панцирем с шипами или без них; ногу, достаточно хорошо развитую, способную сокращаться и оканчивающуюся либо двумя пальцами, либо подобием присоска. Они служат органами временного закрепления. [19]
Во время удара образца о наковальню поворотный барабан с наковальнями остается неподвижным. Это достигается действием специального тормоза. [20]
Во время воздухо-гидравлического удара резина легко разрывается и дает выход воде. Смена такого клапана очень проста и непродолжительна, и клапан легко может быть изготовлен собственными средствами. [21]
За время удара скорости точек системы изменяются на конечную величину. [22]
Поэтому за время удара пренебрегают весом тел и всеми прочими неударными ( конечными) силами, а также перемещениями тел и считают, что векторы скоростей точек ударяющихся тел изменяются мгновенно. [23]
Пусть во время удара на систему наложены новые идеальные обратимые связи. Тогда в ( 15) vv - любой вектор скорости, допустимый для системы с наложенными связями. [24]
Тела во время удара претерпевают деформацию. Сущность удара заключается в том, что кинетическая энергия относительного движения соударяющихся тел на короткое время преобразуется в энергию упругой деформации. Во время удара имеет место перераспределение энергии между соударяющимися телами. Наблюдения показывают, что относительная скорость тел после удара не достигает своего прежнего значения. Это объясняется тем, что нет идеально упругих тел и идеально гладких поверхностей. [25]
Так как время удара очень мало, то можно считать, что пластина не успеет отклониться от вертикального положения и импульс системы как до удара, так и сразу после удара направлен горизонтально. [26]
Руд за время удара т, паз. [27]
В жидкостях во время удара, движения и разбрызгивания ( распыления) возникают большие касательные ускорения на их поверхности, что также приводит к образованию статического электричества. [28]
Следовательно, во время удара сила, которая действовала на мяч, была перпендикулярна стене. [29]
Разделим мысленно все время удара на два промежутка: от момента начала соприкосновения шаров до момента их максимального сжатия и от этого момента до момента прекращения соприкосновения. [30]
Страницы: 1 2 3 4
www.ngpedia.ru
Так бывает в регби, когда один из игроков намеревается приземлить мяч за воротами в зачетном поле… или нет, скорее, пробить штрафной удар. Конечно же речь может идти именно о штрафном ударе, потому что в это время все внимание приковано к нему, наступает главный момент драматургии матча: полная концентрация всех зрителей на каждом его движении. Ему приносят подставку — небольшой пластиковый конус со срезанной верхушкой, простенькая такая конструкция, ничего особенного, но в ней-то все и дело. Вот в это отверстие, в этот «бублик» наверху, он вставляет мяч — так, чтобы заостренный конец овала смотрел в направлении ворот. И сам, замерев на несколько секунд, пристально смотрит туда же: проверяет — попаду, не попаду в эту верхнюю половинку буквы «Н», над перекладиной… И только потом начинается раз и навсегда установленный церемониал: пришло время удара. Несколько шагов назад с той ноги, которая у бьющего «главная», пара в сторону — с «второстепенной»… И — порыв, устремление вперед по дуге! Если это не первая попытка удара, все ритуалы соблюдаются особенно четко — можно сказать, демонстративно…
В Англии в таких случаях телекомментаторы настаивают на том, что вот, мол, какая у них воспитанная публика — по-настоящему спортивная, никто из болельщиков противника не позволяет себе свистеть, орать и тем самым мешать бьющему игроку.
Во Франции, наоборот, сочтут за оскорбление скрывать свистки и вопли, которые только нарастают по мере приближения неизбежного попадания в цель или столь же неизбежного промаха. Свистите, вопите — пришло время удара, во-о-от… вот сейчас…
Бьющий игрок вытирает руки о шорты, отступает для разбега. Под рев болельщиков застывают в напряженных позах судьи у боковых штанг. У каждого в руке флажок. Мяч пролетел между штангами, там, где надо, наверху! Ура! Флажки взлетели вверх!
Если попытка не удалась, тогда «проштрафившийся» машинальным движением отфутболивает куда-нибудь подставку, даже не удостоив ее взглядом. Но если все получилось: мяч прошел, где надо, и команде засчитаны положенные при штрафном три очка, — дальше все совсем иначе. Конечно, регби — игра сугубо мужская, и наивно было бы ожидать проявлений бурной радости — здесь они неуместны: никто не бросается на шею победителю и не сжимает его в объятиях, никто в порыве благодарности Всевышнему не осеняет себя крестом и не целует образок. Если быть точным, то кое-какие знаки — ну, просто мимолетные выражения удовлетворенности — заметить можно. Например, когда нападающий пробегает мимо игрока, только что забившего гол, он легонько шлепает его по заднице. И все. А тот, не обратив на это никакого внимания, бежит на место, и бег его обычен, и в поступи не обнаружишь ничего такого: «А вот смотрите, это ведь я, который…» Разве что в том, как он выбросит с поля подставку для мяча, и материализуется его негромкий триумф. Жест, каким он отправит ее вдаль, приобретет внезапную полноту и властность, он несколько лишних секунд не станет опускать руку… Но главное, главное — это глаза регбиста, взгляд, которым он провожает летящий конус до тех пор, пока тот не коснется земли. Несмотря на краткость всей операции, невольно замечаешь и то, как вытягивается вслед за полетом подставки шея игрока, и то, сколько чувства в этом исполненном одобрения взгляде, ему плевать на полную бессмысленность этого последнего акта… Едва намеченное пространство торжества, приветствие в знак равенства со звездами, равенства, в котором не признаешься и себе самому…
загрузка...
www.ngebooks.com
Cтраница 3
Если же во время удара происходит снятие идеальной обратимой связи, то в ( 15) vv - любой вектор скорости, допустимый для системы до снятия связи. [31]
Хотя место и время удара каждой молекулы о стенку совершенно несущественно, начинать приходится с рассмотрения удара отдельной молекулы. Пока для простоты предположим, что молекулы сталкиваются со стенкой абсолютно упруго. Когда молекула отскакивает от стенки, проекция ее скорости на направление нормали к стенке меняет знак. Обозначим через vx проекцию скорости молекулы до удара, а через v x - vx после удара. Это относится к единичному столкновению. [33]
А теперь пришло время нокаутирующего удара - спокойной ночи, синдром потреблятства. [34]
Во всех рассмотренных моделях время удара бесконечно мало, и его в расчетах принимают равным нулю. Однако с уменьшением жесткости тела время удара занимает все большую часть периода движения тела по лотку, и при расчетах с использованием гипотезы о мгновенности удара появляются слишком большие отклонения по сравнению с экспериментом. Попытка ввести время удара как дополнительную постоянную, как правило, не позволяет ответить на интересующие вопросы. [35]
Импульсами неударных сил за время удара пренебрегаем. [36]
Эти уравнения выполняются во время удара. В послеударном состоянии уравнения ( 15) выполняются, если только вновь наложенные связи сохраняются после удара. [37]
Время действия усилий ( время удара г0) определяется временем пробега волной расстояния от точки удара до ближайшей опоры и обратно - 2, и массой молоточка, а характер их изменения зависит от упругости молоточка. [39]
Импульсами неударных сил за время удара пренебрегаем. [40]
Во всех рассмотренных моделях время удара бесконечно мало, и его в расчетах принимают равным нулю. Однако с уменьшением жесткости тела время удара занимает все большую часть периода движения тела по лотку, и при расчетах с использованием гипотезы о мгновенности удара появляются слишком большие отклонения по сравнению с экспериментом. Попытка ввести время удара как дополнительную постоянную, как правило, не позволяет ответить на интересующие вопросы. [41]
Оказавшихся возле нее во время удара молнии, так как ноги человека оказываются под разностью потенциалов UKI - UK2, которая называется шаговым напряжением Um. [43]
При работе реле во время удара якоря об упоры контакты токовых реле РТ-40 вибрируют. Для гашения вибраций имеется гаситель, представляющий небольшой полый цилиндр, закрепленный на одной оси с якорем и заполненный песком. При срабатывании реле песок поглощает энергию удара якоря об упоры, предотвращая тем самым отскакивание и вибрацию контактов. [45]
Страницы: 1 2 3 4
www.ngpedia.ru
Ударом называется изменения состояния движения тела, вследствие кратковременного взаимодействия его с другим телом. Во время удара оба тела претерпевают изменения формы (деформацию). Сущность упругого удара заключается в том, что кинетическая энергия относительного движения соударяющихся тел, за короткое время, преобразуется в энергию упругой деформации или в той или иной степени в энергию молекулярного движения. В процессе удара происходит перераспределение энергии между соударяющимися телами.
Экспериментальная установка состоит из стального шарика А, подвешенного на проводящих нитях, и неподвижного тела В большей массы, с которым шарик соударяется. Угол отклонения подвеса α измеряется по шкале. В момент удара на шар массой m действует сила тяжести со стороны Земли , сила реакции со стороны нити и средняя сила удара со стороны тела В (см. рис.2.).
